The Treynor ratio is a key metric used by traders and investors to evaluate the risk-adjusted returns of a portfolio. By incorporating beta, a measure of systematic risk, this ratio helps investors determine whether their portfolio’s returns justify the level of market risk taken. Understanding its calculation, significance, and application can enhance investment decision-making (1:2000 leverage broker), particularly for those managing diversified portfolios.
Treynor Ratio Formula and Its Significance
The Treynor ratio is instrumental in assessing a portfolio’s efficiency in generating excess returns relative to its market risk exposure. Unlike the Sharpe ratio, which considers total risk, the Treynor ratio focuses solely on systematic risk, making it particularly useful for well-diversified portfolios.
Understanding the Treynor Ratio Calculation
The Treynor ratio is calculated using the following formula:
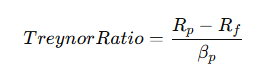
This formula measures how much excess return a portfolio generates per unit of systematic risk. A higher Treynor ratio indicates a more favorable risk-return tradeoff, suggesting that the portfolio delivers higher returns for the level of market risk assumed.
Why Treynor Ratio Matters for Investors
The Treynor ratio plays a crucial role in evaluating fund managers and investment strategies. Key reasons why it matters include:
- Comparing Risk-Adjusted Returns – Investors can use the Treynor ratio to compare funds or portfolios that have different levels of systematic risk.
- Assessing Portfolio Performance – It provides insight into whether a portfolio’s excess return is justified given its exposure to overall market movements.
- Risk Management – By incorporating beta, it helps investors gauge how much return they are earning per unit of market risk, aiding in strategic asset allocation.
For instance, if two funds have identical total returns, but one has a higher beta, the fund with a lower beta will have a higher Treynor ratio, indicating better risk-adjusted performance.
How Treynor Ratio Works in Portfolio Evaluation
Investors rely on the Treynor ratio to measure portfolio efficiency in different market conditions. By isolating systematic risk, it offers a clear view of a portfolio’s ability to generate excess returns without unnecessary exposure to volatility.
Relationship Between Risk, Return, and Beta
Risk and return are inherently linked in investing. The Treynor ratio quantifies this relationship by evaluating:
- Excess Return – The difference between portfolio returns and the risk-free rate.
- Market Sensitivity – Measured by beta, which reflects how much a portfolio’s returns fluctuate relative to the market.
- Risk-Adjusted Performance – The higher the Treynor ratio, the better a portfolio is at delivering returns for the risk it assumes.
For example, a portfolio with a 10% return, a 2% risk-free rate, and a beta of 1.5 would have a Treynor ratio of:
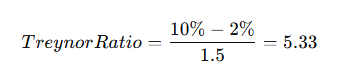
This means the portfolio earned 5.33% excess return per unit of market risk taken.
Interpreting Treynor Ratio Values
Understanding the significance of Treynor ratio values is essential for investment analysis:
| Treynor Ratio | Interpretation |
| Higher Ratio | Indicates strong risk-adjusted performance; the portfolio is generating more return per unit of systematic risk. |
| Lower Ratio | Suggests inefficient risk-taking; the portfolio is not adequately compensating for its market exposure. |
| Negative Ratio | Implies poor performance; either the portfolio lost money or underperformed the risk-free rate. |
When evaluating funds or investment strategies, a consistently high Treynor ratio suggests that a fund manager effectively manages systematic risk while delivering solid returns.
Treynor Ratio Formula Breakdown
To effectively use the Treynor ratio, investors must understand its components and how they influence performance analysis.
Mathematical Representation and Explanation
The Treynor ratio’s formula simplifies risk-adjusted return calculations by focusing on systematic risk. Let’s break it down:
- Portfolio Return – Represents the total gains or losses of an investment.
- Risk-Free Rate – The return an investor would earn with zero risk, such as a 10-year U.S. Treasury bond yield.
- Beta – Measures a portfolio’s volatility relative to the market (e.g., S&P 500). A beta of 1 suggests the portfolio moves in sync with the market, while a beta above 1 indicates higher volatility.
The formula effectively tells investors:
- How much return is generated above the risk-free rate (numerator).
- How much market risk was taken to earn that return (denominator).
Role of Beta in Systematic Risk Assessment
Beta is central to the Treynor ratio as it quantifies systematic risk—the risk that cannot be eliminated through diversification. Key insights about beta’s role include:
- Beta of 1.0 – Portfolio moves in line with the overall market.
- Beta greater than 1.0 – Portfolio is more volatile than the market.
- Beta less than 1.0 – Portfolio experiences lower volatility than the market.
For example, a hedge fund with a 15% return, a 3% risk-free rate, and a beta of 0.8 would have a Treynor ratio of:
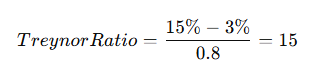
Since the portfolio’s beta is less than 1, it has delivered strong risk-adjusted returns with less volatility than the market. This is an ideal scenario for conservative investors seeking steady performance.
Treynor Ratio vs. Sharpe Ratio: Key Differences
Both the Treynor ratio and Sharpe ratio are widely used for evaluating risk-adjusted returns, but they differ in how they measure risk. Understanding their distinctions helps investors select the most suitable metric based on their portfolio composition and investment strategy.
Measuring Risk-Adjusted Returns in Different Ways
The fundamental difference between these two ratios lies in their approach to risk measurement:
| Metric | Treynor Ratio | Sharpe Ratio |
| Risk Considered | Systematic risk (measured by beta) | Total risk (measured by standard deviation) |
| Best For | Diversified portfolios | Portfolios with both systematic and unsystematic risk |
| Interpretation | Measures return per unit of market risk | Measures return per unit of total risk |
The Treynor ratio is particularly useful when analyzing well-diversified portfolios because it focuses only on systematic risk, assuming that unsystematic risk has been diversified away. Meanwhile, the Sharpe ratio considers both systematic and unsystematic risk, making it more appropriate for portfolios with concentrated holdings.
Choosing the Right Ratio for Portfolio Analysis
Selecting between the Treynor and Sharpe ratio depends on an investor’s portfolio structure:
- For diversified investors – The Treynor ratio is preferable because it evaluates returns relative to systematic risk, which is the primary concern for broad-market portfolios.
- For non-diversified investors – The Sharpe ratio is better suited as it considers total risk, making it useful for individual stocks or concentrated investments.
- For fund managers – The choice depends on the strategy. Actively managed funds may prefer the Sharpe ratio, while passive index investors might rely on the Treynor ratio to measure risk-adjusted returns.
Advantages and Limitations of Treynor Ratio
The Treynor ratio provides valuable insights into portfolio performance, but it has limitations that investors must consider.
Benefits in Portfolio Performance Evaluation
- Effective for comparing diversified portfolios – Since it focuses on systematic risk, the Treynor ratio allows investors to compare portfolios with different levels of market exposure.
- Helps assess fund manager efficiency – A higher Treynor ratio suggests that a fund manager is effectively generating returns relative to the portfolio’s beta.
- Useful for strategic asset allocation – Investors can use the ratio to evaluate whether they are being adequately compensated for the level of risk they take in various asset classes.
Drawbacks and Potential Misinterpretations
- Assumes a well-diversified portfolio – If a portfolio has significant unsystematic risk, the Treynor ratio may give an incomplete picture of performance.
- Dependent on beta accuracy – Since beta measures past market sensitivity, it may not always reflect future risk exposure accurately.
- Ignores downside volatility – Unlike the Sortino ratio, which focuses only on downside risk, the Treynor ratio does not distinguish between upside and downside movements.
Treynor Ratio in Practice: Example Calculation
Applying the Treynor ratio to real-world portfolios allows investors to assess its practical significance.
Step-by-Step Calculation Using a Sample Portfolio
Portfolio details:
- Portfolio return = 12%
- Risk-free rate = 3%
- Portfolio beta = 1.5
Treynor Ratio Calculation:
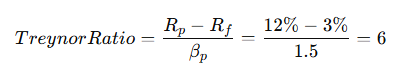
This means the portfolio earns 6% excess return per unit of market risk taken.
Insights Gained from Treynor Ratio Results
- Higher Treynor Ratio: A fund with a Treynor ratio of 8 would be considered more efficient than one with a Treynor ratio of 5, assuming they operate in similar markets.
- Negative Treynor Ratio: If a portfolio’s return is lower than the risk-free rate, the Treynor ratio becomes negative, indicating poor performance relative to risk.
- Comparing Multiple Funds: Investors analyzing different funds with similar market exposure can use the Treynor ratio to determine which offers better risk-adjusted returns.
Factors Influencing Treynor Ratio Accuracy
The Treynor ratio provides valuable insights into risk-adjusted returns, but its accuracy depends on several external factors. Understanding these influences ensures investors can correctly interpret the ratio and apply it effectively in portfolio management.
Impact of Market Volatility on Treynor Ratio
Market volatility plays a significant role in shaping the Treynor ratio as it directly affects beta, the key risk component in its formula. High volatility can distort beta measurements, leading to misleading conclusions about a portfolio’s risk-adjusted performance.
Key impacts of volatility on Treynor ratio accuracy:
- Rising volatility increases beta, which may lower the Treynor ratio despite strong returns.
- Sharp market corrections can cause temporary spikes in beta, making a historically stable portfolio appear riskier than it actually is.
- Low-volatility markets can lead to understated risk assessments, inflating Treynor ratio values beyond realistic expectations.
To address these distortions, investors should analyze the ratio over multiple market cycles rather than relying on a single period’s data.
Adjustments for Different Asset Classes
The Treynor ratio is primarily used for equity portfolios, but applying it to different asset classes requires careful adjustments:
| Asset Class | Considerations for Treynor Ratio Accuracy |
| Equities | Beta is a widely accepted risk measure, making the Treynor ratio highly applicable. |
| Fixed Income | Bonds have lower volatility and may have a near-zero beta, making the ratio less meaningful. |
| Commodities | Prices are influenced by external factors like supply and geopolitical risks, requiring adjusted beta calculations. |
| Alternative Investments (Hedge Funds, Private Equity) | Low liquidity and infrequent pricing can distort beta, affecting Treynor ratio reliability. |
To improve accuracy, investors should compare Treynor ratios within the same asset class rather than across different markets.
Best Use Cases for Treynor Ratio in Trading
While the Treynor ratio is commonly used in portfolio analysis, its effectiveness varies depending on the context. It is most useful when comparing diversified investments exposed to systematic risk.
Applying Treynor Ratio in Mutual Fund Analysis
Mutual funds are one of the best use cases for the Treynor ratio since they are typically well-diversified. Investors can use the ratio to:
- Compare risk-adjusted returns between funds with different levels of market exposure.
- Evaluate fund manager efficiency in generating returns relative to systematic risk.
- Assess whether higher beta funds provide sufficient compensation for their increased market exposure.
For example, if Fund A has a Treynor ratio of 0.8 and Fund B has 0.5, Fund A delivers superior risk-adjusted returns despite similar market exposure.
Evaluating Portfolio Risk in Various Market Conditions
Investors use the Treynor ratio to assess portfolio performance under different market scenarios:
- Bull Markets: A high Treynor ratio indicates the portfolio efficiently captures upside gains relative to market risk.
- Bear Markets: A low or negative Treynor ratio suggests the portfolio fails to compensate for its systematic risk exposure.
- Sideways Markets: Beta remains relatively stable, making the ratio a useful measure of return consistency.
By analyzing the Treynor ratio across different economic cycles, investors can refine risk management strategies and ensure long-term stability.
Frequently Asked Questions on Treynor Ratio Formula
How Does Treynor Ratio Differ from Other Risk Metrics?
The Treynor ratio differs from similar risk-adjusted performance measures in the way it defines risk:
| Metric | Risk Considered | Best Used For |
| Treynor Ratio | Systematic risk (beta) | Well-diversified portfolios |
| Sharpe Ratio | Total risk (standard deviation) | Any portfolio, including concentrated ones |
| Sortino Ratio | Downside risk | Evaluating portfolios with asymmetrical return distributions |
The Treynor ratio is ideal when systematic risk is the primary concern, whereas the Sharpe ratio is better for assessing overall volatility.
What Is Considered a Good Treynor Ratio?
A higher Treynor ratio suggests stronger risk-adjusted performance, but what qualifies as “good” depends on market conditions and investment objectives.
- Treynor ratio > 0.5 – Indicates efficient risk-adjusted returns.
- Treynor ratio < 0.2 – Suggests low compensation for systematic risk.
- Negative Treynor ratio – Implies underperformance, meaning the portfolio’s return is lower than the risk-free rate.
Comparing a fund’s Treynor ratio to its benchmark provides better insight than analyzing it in isolation.
When Should Investors Use Treynor Ratio?
The Treynor ratio is most useful when:
- Assessing actively managed funds that take varying levels of market risk.
- Comparing portfolios with different risk exposures but similar asset allocations.
- Analyzing performance in volatile markets to see if excess risk-taking is justified by higher returns.
